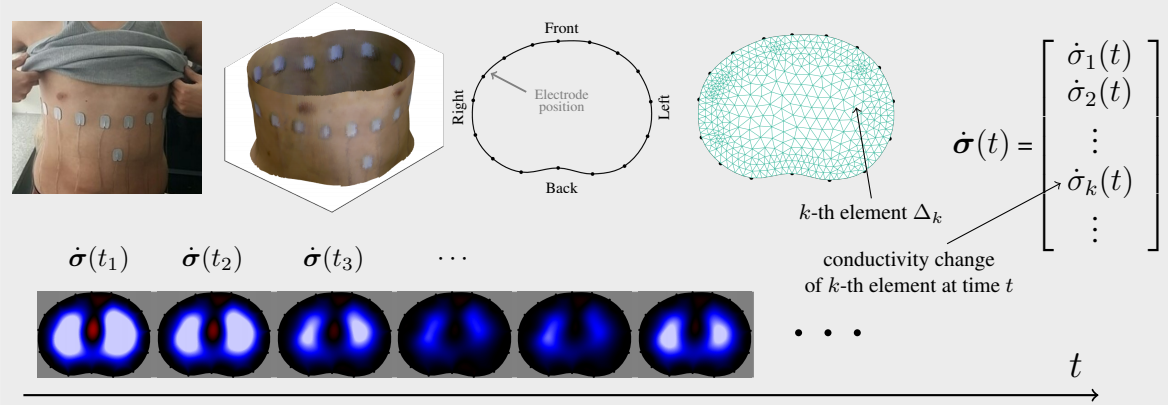
Electrical impedance tomography (EIT) provides functional images of an electrical conductivity distribution inside the human body. Since the 1980s, many potential clinical applications have arisen using inexpensive portable EIT devices. EIT acquires multiple trans-impedance measurements across the body from an array of surface electrodes around a chosen imaging slice. The conductivity image reconstruction from the measured data is a fundamentally ill-posed inverse problem notoriously vulnerable to measurement noise and artifacts. Most available methods invert the ill-conditioned sensitivity or the Jacobian matrix using a regularized least-squares data-fitting technique. Their performances rely on the regularization parameter, which controls the trade-off between fidelity and robustness. For clinical applications of EIT, it would be desirable to develop a method achieving consistent performance over various uncertain data, regardless of the choice of the regularization parameter. Based on the analysis of the structure of the Jacobian matrix, we propose a fidelity-embedded regularization (FER) method and a motion artifact reduction filter. Incorporating the Jacobian matrix in the regularization process, the new FER method with the motion artifact reduction filter offers stable reconstructions of high-fidelity images from noisy data by taking a very large regularization parameter value. The proposed method showed practical merits in experimental studies of chest EIT imaging.
A Fidelity-Embedded Regularization Method for Robust Electrical Impedance Tomography